Problem Statement and Motivation:
Our goal for this project is to build a recommender system for restaurants using publicly available Yelp data. Our motivation is to understand the function of these systems and implement our own approaches based on what we learn from the EDA and what we have learned in the course thus far.
Introduction and Description of Data:
Recommender systems are present in almost every popular website and app today. Most recently they have received a great deal of media attention due to the way that news articles and other web content is served to users based on their previous online behavior. The most challenging aspect of this project was ensembling the different models we built. We found many different approaches to this problem online and many were good at producing recommendations in certain circumstances, but comparing the different types of error metrics and deciding what to implement into our pipeline was one of the hardest parts.
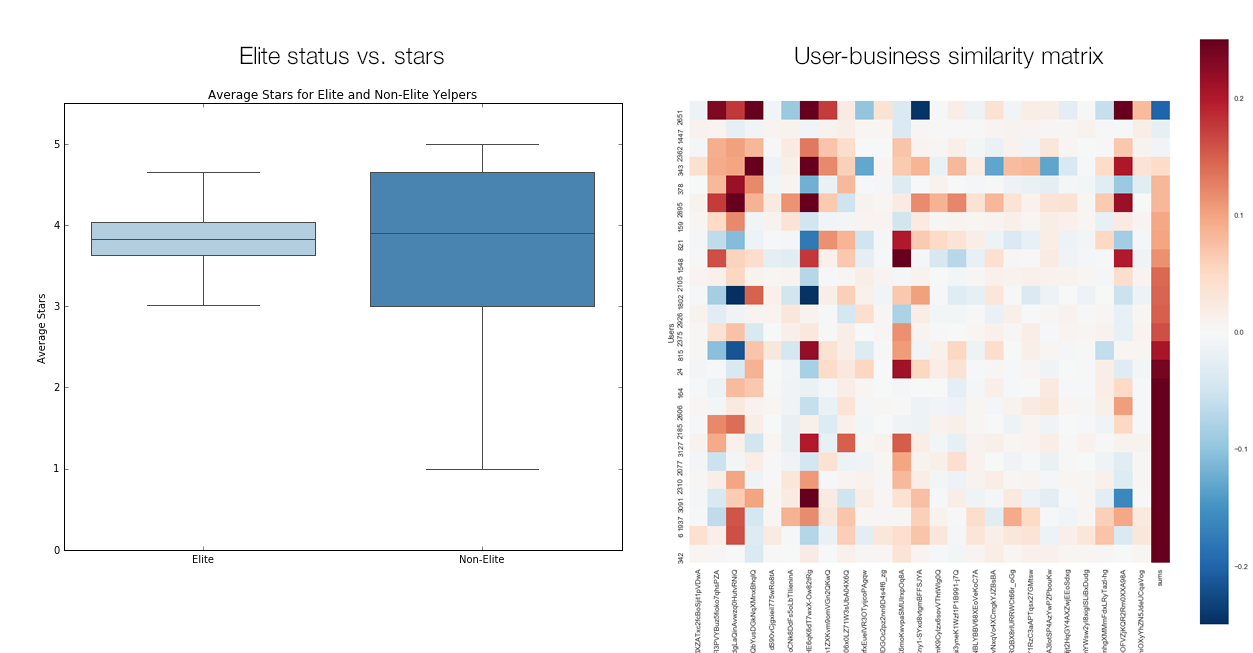
Our preliminary EDA revealed that the population of “elite” users within the community of Yelp reviewers introduced some interesting patterns in the data. We found that although elite users only accounted for a small fraction of the total users, they contributed almost half of the restaurant reviews. We also found that the distribution of the star ratings given by elite users was smaller, and the mean was higher. Due to this, we decided to create an additional binary predictor in our dataset that is set true if a user was ever listed as elite.
The literature sources we found during our preliminary research primarily described models developed for the Netflix prize. The winning model developed by the BellKor team was extremely complex, but the authors made it clear that the core of their model’s success was due to the simple baseline strategy that they spent a great deal of time refining. The complex ensembling and boosting algorithms they used only accounted for a few percentage points in performance increase. We decided to take the same approach and focus a large portion of our efforts on our baseline and then build on top of it.
Literature Review/Related Work:
[1] Matrix Factorization for Movie Recommendations in Python. (2016, November 10). Retrieved December 8, 2017, from https://beckernick.github.io/matrix-factorization-recommender/
[2] Spark, C. (n.d.). Implementing your own recommender systems in Python. Retrieved December 8, 2017, from
[3] Winning the Netflix Prize: A Summary. (n.d.). Retrieved December 8, 2017, from http://blog.echen.me/2011/10/24/winning-the-netflix-prize-a-summary/
Modeling Approach and Project Trajectory:
Our EDA phase showed us that cities and neighborhoods have independent means and distributions. We would have to filter our recommendations by location for functional recommendation purposes anyways, so we decided to build our data filtering first around cities. Once we select a city, we focus on the reviews data set, and remove any rows from users that occur less than five times to prevent the “cold start” problem.
-
Baseline model 1( arithmetic) - We adapted a method we learned from the Netflix prize paper and calculated the deviations from the global mean for each user and business in the dataframe. We initially thought we would supplement use a KNN based collaborative filtering model to supplement our arithmetic baseline, but we found that matrix factorization served the save purpose and was simpler to implement.
- Baseline model 2 (ridge regression):
- In the ridge model, we use indicator variables for the u-th user and m-th item that go into the feature matrix to predict on the stars in the reviews dataset.
- Collaborative filtering with user-user + restaurant-restaurant similarity matrices
- We implemented a collaborative filtering methods that uses a user-user matrix and a restaurant-restaurant matrix to calculate how each user deviates from the mean of the dataset based their similarity to other users and other restaurants. We used svd (singular value decomposition) for matrix factorization and cosine similarity for similarity matrices
- This method generally produce good results but are not good for cold-start problems in which cases the users have not rated any restaurants
Initial baselines from arithmetic mean prediction and Ridge Regression were used as predictors an ensemble regression model. An ensemble model was constructed by averaging the output predictions of each model. This mean-ensemble model outperformed both individual models as quantified by RMSE.
Linear Regression, Ridge Regression, Lasso Regression, K-Nearest-Neighbors (KNN), and Random Forest approaches were also trained on the predictions of the arithmetic and Ridge models to predict the target star value. For Random Forest and KNN models, neighbor and estimator counts were tuned to find a minimum RMSE value on the test set. Of each of these models, Ridge Regression scored obtained the lowest RMSE followed by Linear Regression and outperformed the mean-ensemble model.
The predictions of these models were in turn used to create a second meta-model. KNN and Random forest estimators were excluded from this due to exceptionally poor RMSE scores. A Ridge Regression model was subsequently trained using the outputs of the Linear, Ridge, Lasso, and previous baseline predictions as predictors. Ridge Regression was selected due to its consistently low RMSE values. This meta-model did not outperform the previous ensemble method and the original Ridge-Regression based ensemble method was selected as a baseline model.
The model was able to be improved by the incorporation of single-variable-decomposition (SVD) into the Ridge-Regression based ensemble model. Because of this, the final implemented model is comprised of a Ridge Regression model trained on the estimated ratings provided by a separate Ridge Regression model, arithmetic mean predictions, and SVD predictions. These baseline models were trained on almost all available user and business data. The final achieved RMSE of this model was 0.727.
Results, Conclusions, and Future Work:
Through the generation of an ensemble model that combined Ridge Regression, arithmetic mean estimation, and SVD, we were able to achieve a test set RMSE value of 0.749. The accuracy of this model was higher than any single tested regression model and had a comparable test-set RMSE value to similar recommenders such as those constructed for the Netflix prize.
It is possible that the constructed model could be improved through the more effective separation of baseline and latent factors. In the described model, the baseline estimators were trained using most available user and business data. These models were then combined using Ridge Regression. Other recommender systems have been trained through the separation of baseline and latent factors. In these systems, a baseline is constructed as a global or local average and latent factors consist of user specific interaction terms, business specific interaction terms, and other combination terms. These latent factors can account for scenarios where a specific user may typically rate 0.5 stars below the global mean or a specific restaurant tends to score 0.5 stars above the global mean. Once these baseline and latent factors are computed, the final interaction term can act as a residual for the training of a regression model. Separation of the model’s components in this manner may yield improved results.
An alternative approach to this challenge would be to construct a classification model rather than a regression model. In this method, the star ratings would be treated as five separate classifications. Rather than regression models, classification models would be used in order to boost the classification accuracy of the model. Implementing this method would require the use of a separate scoring system than RMSE and does not necessarily account for the progressive rating of the star system. However, it is reflective of the user system in which only ratings of one, two, three, four, or five stars can be entered into the model.
Given enough time, the model could always be improved through experimentation with different regression methods and data structures. Weighting the similarity of users in different manners such as constructing neighborhoods could allow for more accurate predictions, while a more complex ensemble method such as that constructed for the Netflix prize may further improve the system. Ultimately, altering the parameters of the baseline estimators would likely have the largest impact on the effectiveness of the model. This is a matter of further exploring the optimal combination of these estimators in order to improve the model’s accuracy.